Memória e Guia para a Réplica da oficina realizada no Festival da Matemática 2017, Rio de Janeiro, 27 a 30 de abril. [Veja o programa]
A oficina pretende aproximar os participantes aos fundamentos geométricos das mandalas e dos tesselados de forma prática e criativa.
Através de exemplos, serão apresentados conceitos de geometria ornamental e elementos teóricos sobre os grupos de simetria.

• INTRODUÇÃO: Geometria, arte islámica e o trabalho de M.C. Escher
• MANDALAS E ROSETAS: Simetria radial
• TESSELADOS: Ladrilhos, azulejos... e muito mais
• FAÇA VOCÊ MESMO: Imitando os mestres
• APENDENDO DO ESCHER: Aplicando a matemática na arte
• FAÇA VOCÊ MESMO: Está na hora de criar
• RECAPITULANDO: Grupos de simetria, isometrias e notação
• RECURSOS: Faça você mesmo (material de apoio)
• REFERÊNCIAS: Há muito mais que aprender

Em todas as culturas encontramos ornamentos e objetos artísticos que apresentam simetria. Os nossos ancestros começaram imitando as formas geométricas que observavam na natureza, mas ao longo da história foram criando seus próprios símbolos, suas próprias figuras e ornamentos de caráter progresivamente mais abstrato e complexo.

Figura 1. Exemplos de arte geométrica, presente em artefatos e na arquitetura.

Algumas culturas desenvolveram ornamentos geométricos mais do que outras, é o caso do mundo islámico, onde a partir da proibição (mesmo que implícita) da representação pictórica de seres vivos, criaram-se elaborados ornamentos geométricos que representassem a grandiosidade da sua espiritualidade, e sua cultura, adornando templos e palácios.

Figura 2. Alhambra, Granada, Espanha.

As culturas espanhola e portuguesa tem uma grande influência árabe devida à longa ocupação do sur da península ibérica (Al-Ándalus, 711-1492). Um dos principais monumentos da ocupação islámica na região é a cidadela da Alhambra, um complexo de palácios, jardins e fortaleza situado em Granada, Espanha. Patrimônio da Humanidade, é visitado cada ano por milhões de turistas do mundo inteiro.

A Alhambra tem servido de inspiração para muitos artistas ao longo dos anos, um deles, ficaria fascinado pela divisão regular do plano encontrada em muitos dos motivos ornamentais do palácio e desenvolveria ao longo da sua vida um total de 137 desenhos com divisões regulares do espaço.
Se trata de Maurits Cornelius Escher (1898-1972) [1], quem se tornaria famoso por esses trabalhos e por outros onde representa construções impossíveis, ilusões da perspectiva e divisões regulares de espaçoes esféricos e hiperbólicos.

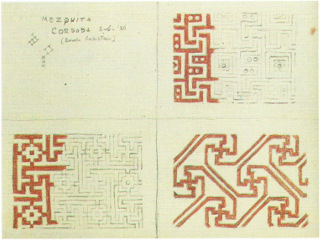
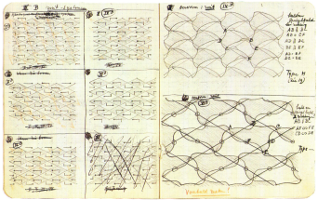
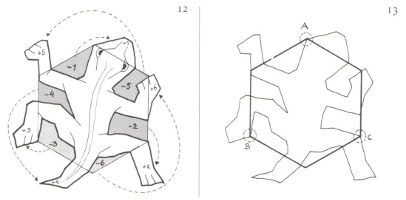
Figura 3. Rascunhos de arte mourisca, realizados por M.C.Escher e sua esposa Jetta (SCHATTSCHNEIDER, 1990).

Iremos a explorar dois tipos de ornamentos geométricos e suas construções:

Mandalas

Diagrama, geralmente circular e com formas geométricas, que representa o universo. [*]
Os desenhos tem se popularizado pela sua presença em livros para colorir para adultos e a sua disposição circular possibilita de forma natural as simetrias rotacionais.
No mesmo conjunto de ornamentos com simetria rotacional se encontram as rosetas ou rosáceas e os nós celtas, entre outros.
[Ir para a secção]

Tesselados

O termo não existe desta forma em português, mas se deriva do inglês tesselation, e é congruente com o português tessela [*]:

1. Pedra quadrada para lajear compartimentos de um edifício.
2. Cubo ou peça de mosaico.

1. Traslação.
2. Rotação.
3. Reflexão.
4. Reflexão deslizante (que é equivalente a uma reflexão seguida de uma traslação).

Voltar ⇧

• Escolha o número de folhas de simetria você quer e configure o tamanho da malha.
• Imprima ou exporte a PDF, as legendas não aparecerão na sua impressão.
• Acesse o aplicativo: 🖶 Simetria radial

Voltar ⇧

Há infinitas formas de cubrir o plano com tesselas geométricas repetidas periodicamente. Para classificá-las, elas são organizadas pela forma em que são construidas através das isometrias: traslações, reflexões, rotações e reflexões deslizantes.
Os grupos em que são classificadas chamam-se de grupos cristalográficos, devido a que sua generalização em 3D modela a formação de cristais na natureza.
Todos os grupos compartilham o fato de ter duas tralações às quais são invariantes, este fato é o que faz com se conheçam como tesselados periódicos regulares. Também sabemos, graças ao Teorema de Fedorov (1891), que as únicas rotações possíveis são as de 180°, 120°, 90° e 60°.
Os grupos estão fortemente relacionados entre eles, isto é, uns ficam contidos dentro de outros, por esse motivo é fácil ao tentar classificar um ornamento, colocá-lo num grupo mais geral ao qual realmente pertence.
Nos ornamentos da Alhambra se encontram presentes os 17 grupos de simetria [*]. Se tiver interesse, pode encontrar os desenhos explicados aqui.

Na primeira parte apresentaremos os grupos com reflexões, reflexões deslizantes e rotações de 180°. Passíveis de ser construídos com malhas paralelas.

Nesta seguna parte serão apresentados os grupos que apresentam rotações de 90°, 120° e 60°, e que complementam as possibilidades para a divisão regular do plano de forma periódica.

Voltar ⇧

Para começar a sua própria pratica, uma etapa importante é aprender a reproduzir desenhos clássicos, com muita atenção, para poder descobrir os detalhes da construção e as simetrias presentes nos desenhos.
Já observamos como o próprio Escher começou copiando com atenção e cuidado os desenhos na Alhambra, para depois criar suas próprias obras a partir deles.

Clique para aumentar

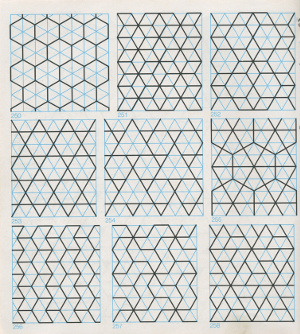
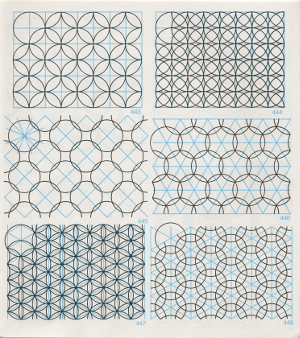
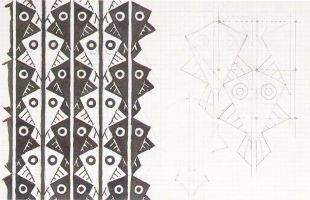
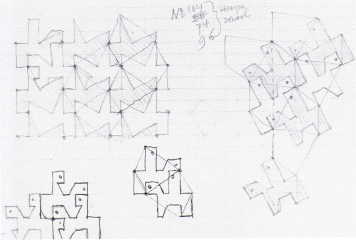
Figura 4. Arte mourisco: desenhos e diagramas para sua análise (WADE, 1992) [Veja mais]

• Escolha o desenho da sua preferência da galeria.
• Reproduça o desenho com ajuda da grade impressa.
• Tente identificar:
  1. As traslações, necessárias para verificar que o desenho é periódico.
  2. Todas as simetrias presentes: reflexões, rotações e reflexões deslizantes.
  3. A região mínima a partir da qual se constrói o desenho.
  4. Finalmente, o grupo de simetria ao qual pertence.
• Configure o tamanho da malha e as orientações das linhas na grade.
• Imprima ou exporte a PDF, as legendas não aparecerão na sua impressão.
• Acesse os aplicativos: 🖶 Malha paralela / 🖶 Malha isométrica

Voltar ⇧

M.C.Escher desenvolveu a tal grau a sua técnica de divisão regular do plano, que foi ele mesmo o primeiro em colocar questões sobre os efeitos da cor nos grupos de simetria, por exemplo. Ele manteve frequentes encontros com cientistas e matemáticos para dialogar sobre as suas ideias e suas criações.

Figura 5. Rascunhos e figuras anotadas nos cadernos de M.C.Escher (SCHATTSCHNEIDER, 1990).

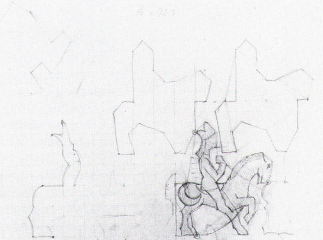
A sua técnica foi desenvolvida com a cuidadosa observação das características dos tipos de simetria e as relações das tesselas (os elementos unitários) que as isometrias lhes impõem, como podemos observar na seguinte figura.

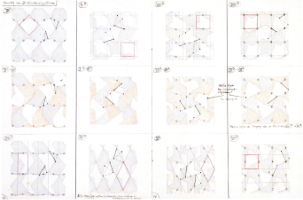
Figura 6. Processo criativo da Divisão Regular No. 67 Horsemen, M.C.Escher, 1946 (SCHATTSCHNEIDER, 1990).

Voltar ⇧

Agora é a sua vez de transformar um tesselado comum e transformar ele num mundo a parte, cheio de suas criações.

1. Configure a sua malha e imprima: 🖶 Malha paralela / 🖶 Malha isométrica
2. Escolha um dos grupos de simetria, para facilitar, pode consultar a Tabela de Resumo.
3. Observe que as transformações a ser aplicadas à tessela-base deverão ser replicadas corretamente no resto do desenho (observe que a própria tessela base pode afetar lados opostos ou adjacentes), comece com a tessela-base e os vizinhos imediatos. Se estiver com dúvidas do que isso significa, veja com cuidado a Secção anterior.
4. Esta etapa é a que mais trabalho implica, mas vai com paciência e inspiração. Escolha desafios simples no início, isto lhe permitirá aprofundar o seu conhecimento dos grupos de simetria para criar desenhos mais complexos de forma progressiva.

Voltar ⇧

Voltar ⇧

🖶 Colocamos à sua disposição uma série de aplicativos que geram os materiais impressos utilizados na oficina. Com eles você dispõe de uma malha de suporte para personalizar as suas criações, podendo reproduzir e distribuir para trabalhar na sala de aula ou em casa. Só selecione os parámetros desejados e imprima:

🖶 Simetria radial

🖶 Paralelogramos

🖶 Isométrico

Voltar ⇧

Referências bibliográficas	Recursos na web	Aplicativos
COXETER, H.S.M.; MOSER, W.O.J.; 1980 (4a). Generators and Relations for Discrete Groups. ESCHER, M.C.; 1972. Le monde de M.C. Escher: l'oeuvre de M.C. Escher (commenté par J.L. Locher). SUTTON, Daud; 2007. Islamic Design: A genius for geometry. GRÜNBAUM, Branko; SHEPARD, G.C.; 1987. Tilings and Patterns. KAPLAN, Craig; 2009. Introductory Tiling Theory for Computer Graphics. SCHATTSCHNEIDER, Doris; 1990. Visions of symmetry : notebooks, periodic drawings, and related work of M.C. Escher. WADE, David; 1982. Geometric Patterns & Borders.	17 Wallpaper Groups Art of the Islamic World: A Resource for Educators. Edited by Maryam D. Ekhtiar and Claire Moore. Islamic Art and Geometric Design. Activities for Learning. The Metropolitan Museum of Art. M.C.Escher Oficial Website. Pattern in Islamic Art. WADE, David; 2017. Symmetry and Ornament. JABLAN, Slavik; 1995. Tiling Encyclopedia. FRETTLÖH, Dirk.	Os vídeos desta página foram criados com: MUAN, Manipulador Universal de ANimações Anima Mundi - IMPA - IBM Para criar simetrias no dispositivo móvil: Kaleidopaint (Android & IOS) WEEKS, Jeff.

Voltar ⇧